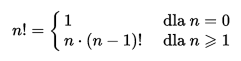RekurecjaCzęść NR.9 W funkcjonalnych językach programowania rekurencja jest narzędziem z dużą tradycją. Wiele oryginalnych języków funkcjonalnych nie miało konstrukcji pętli. W takich wypadkach była używana rekurencja.
Obecnie wiele języków funkcjonalnych ma definicję pętli w swojej składni.
Nie zmienia to jednak faktu, że rekurencja wciąż jest używana przez wielu programistów.
Rekurencja
w C# używanie rekurencji nie jest zalecane ze względu na to, że optymalizacja rekurencji ogonowej nie zawsze występuje w tym języku.
Mimo wszystko warto poznać główną ideę rekurencji, w końcu wiele algorytmów z niej korzysta.
Oto przykładowa implementacja silni, która jest doskonałym przykładem rekurencji.
static int Factorial(int x)
{
if (x == 0)
return 1;
return x * Factorial(x - 1);
}Silnia z 4! to 1 * 2 * 3 * 4 = 24. Silnia z 3! to 1 * 2 * 3 = 6.
Jak widzisz istnieje pewien wzór do liczenia silni. Każda liczba z “n” jest zdefiniowana wywoływaniem do metody Factorial z parametrem n. Potem metoda uruchamia jeszcze raz tę samą metodę z parametrem n – 1.
Dla liczby 3 wywołanie będzie wyglądało tak 3 * Factorial(2) . Wywołanie metody Factorial(2) ponowi ten sam proces i wykona 2 * (Factorial)
Ten proces mógłby trwać w nieskończoność, gdyby nie fakt, że ponowne wywoływanie metody jest przerwane warunkiem.
Ten warunek nazywa się bazową wartością rekurencji, która ma zatrzymać łańcuch wywołań. Każde wywołanie metody rekurencyjnie powinno zmienić jakiś parametr – jeśli tak nie jest to zapewne coś robimy źle i mamy niekończącą się pętlę
Silnia z zero daje jeden i zatrzymuje wywołanie silni. Sama funkcja też nie jest idealna, w końcu zakładamy, że użytkownik będzie podawał liczby nieujemne.
Oto co się dzieje, gdy wywołamy silnie z parametrem 3.
int r = Factorial(3);
Wywołanie: Factorial(3) --> n = 3
Czy jest n == 0? --> NIE
return Factorial(2) --> n = 2
Czy jest n == 0? --> NIE
return Factorial(1) --> n = 1
Czy jest n == 0? --> NIE
return Factorial(0) --> n = 0
Czy jest n == 0? --> TAK
return 1
return 1 * 1 --> 1
return 2 * 1 --> 2
return 3 * 2 --> 6
return 6;
Implementacja funkcji rekurencyjnej jest elegancka, bo reprezentuje matematyczny wzór.
Niestety rekurencja nie zawsze jest użyteczna z punktu widzenia wydajności.
W C# implementacja silni w formie pętli będzie bardziej wydajna. Pętla eliminuje wywołania funkcji i i zwracanie przez nią zawartości .
private static int Factorial(int x)
{
int y = x;
for (int i = x - 1; i > 1; i--)
{
y = y * i;
}
return y;
}Pętla może być czasem mniej czytelna, ale w C# będzie ona bardziej wydajna. Kompilator w C# nie zawsze optymalizuje wywołania rekurencyjne.
Rekurencja ogonowa i jej optymalizacja
Inne języki programowania zwłaszcza te funkcjonalne potrafią optymalizować wywołania rekurencyjne. Co sprawia, że pętla i rekurencja będą się wykonywać tak samo wydajnie.
W czym jest dokładnie problem z rekurencją. Otóż cała sieć wywołań rekurencji, chociażby silni musi po pierwsze pamiętać wszystkie wartości zmiennych na każdym poziomie wywołania.
1000 razy wykonana rekurencja oznacza 1000 krotne zapamiętanie wszystkich zmiennych, jakie są używane w metodzie.
Factorial(99999999);
Dokładna implementacja i rozmieszczenie pamięci jest zależne od języka, ale zazwyczaj dzieje się to w stosie, który przetrzymuje funkcje. Te funkcje wraz z ich zmiennymi są potem czyszczone ze stosu w odwrotnej kolejności.
Istnieją tutaj dwa problemy. Po pierwsze wywołanie funkcji i zwrócenie jej wartości jest bardziej kosztowne niż proste wywołanie tego samego kodu, bo to wymaga operacji na stosie.
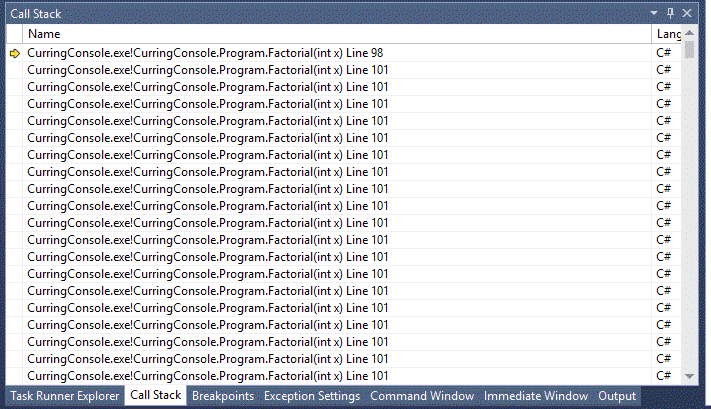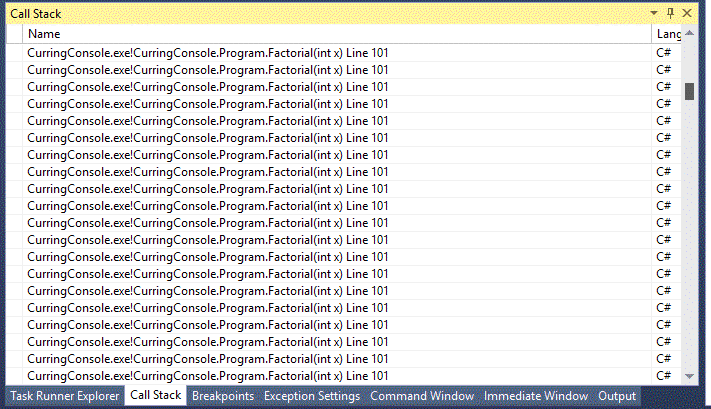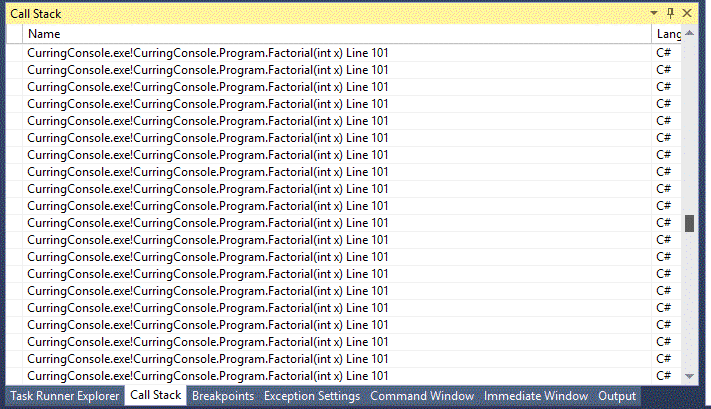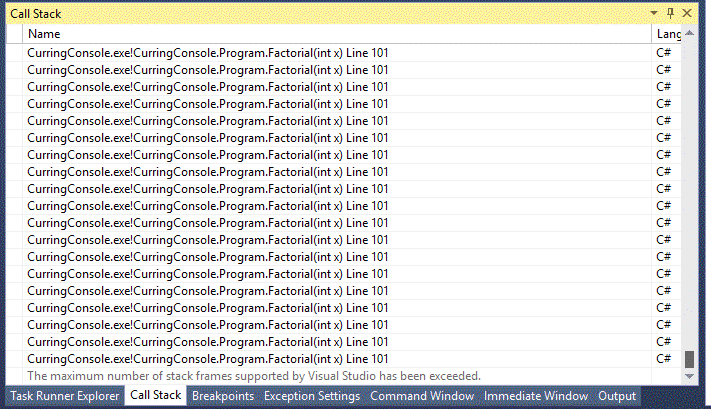
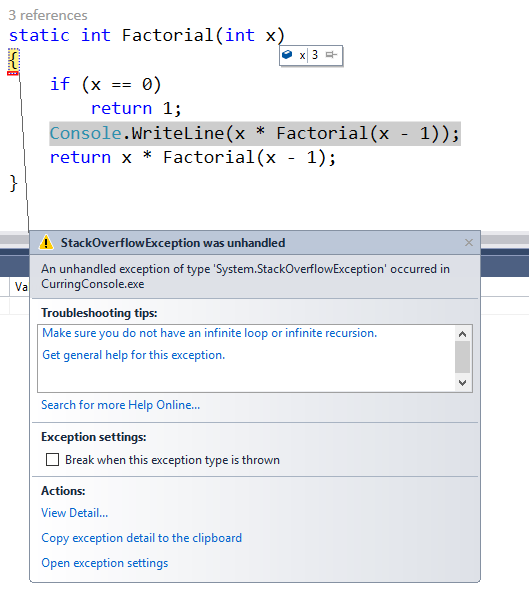
Po drugie pamięć na stosie jest ograniczona.
Co zakończy się wyjątkiem StackOverflowException. Co ciekawe wykonanie pętli tyle samo razy by otrzymać wynik silni nie zwróci mi tego błędu, ale wynika to z mechanizmu działania, który właśnie przed chwilą omówiłem.
Optymalizacja rekurencji polegałaby na usunięciu operacji wracających, czyli na ogonie rekurencji.
Kompilator rozpoznaje, że rekurencja ogonowa jest wykonywana i nic nie robi. Dodaje więc on swój własny skok przez wszystkie wywołania zwracając właściwą wartość.
Ta optymalizacja usuwa problemy pamięciowe na stosie, gdy sekwencje wywołań są bardzo długie.
Optymalizacja w C# jest trochę problematyczna. CLR posiada w sobie instrukcje optymalizacji rekurencji, ale nie jest ona używana przez kompilator C#. Inne języki jak np. F# potrafią z niego korzystać.
Dla C# pojawia się jeszcze jedna szansa na optymalizację, gdy pracujemy nad aplikacją 64-bitową.
W .NET mamy jeszcze kompilator JIT, który dla aplikacji 64-bitowych w C# dodaje tę instrukcję. Niestety dla aplikacji 32-bitowych tego nie robi.
Ostatecznie więc używanie rekurencji w C# jest niezalecane. Zwłaszcza gdy wiemy, że będziemy mieć wiele wywołań tej samej funkcji.