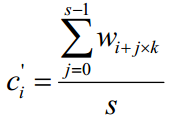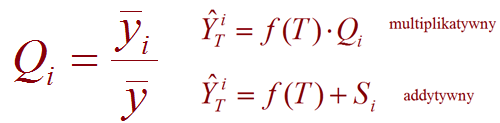Wsykaźnik W poprzednim wpisach wygładziliśmy szereg czasowy mechanicznie za pomocą średnich ruchomych jak i przy pomoc funkcji liniowej trendu.
Mając już funkcje liniową trendu jesteśmy także wstanie przenalizować wahania okresowe.Do egzaminu z tej dziedziny muszę jeszcze zapoznać się z analizą wahań okresowych.
Szereg czasowy o“n” okresach w tym przypadku “12” dzielimy na “S” cykli.
Działania mające na cel wyodrębnienia wahań okresowych są następujące.
- Wygładzamy szereg czasowy “yt”. Najlepiej przy pomocy funkcji trendu. Przy pomocy funkcji trendu obliczamy wartości teoretyczne.
- Obliczamy “wielkość wahań okresowych”. Jest to ułamek “wartości szeregu czasowego” przez “wartość teoretyczne”.
- Później na podstawie wskaźnika wahań okresowych wyliczamy średnią arytmetyczną jednoimiennych okresów (w tym wypadu są to kwartały). Są to surowe wskaźniki sezonowości.
- Suma takich wskaźników dla wszystkich faz powinna być równa “k” czyli dla kwartałów jest to liczba “4” bo mamy 4 kwartały w roku. Jeżeli suma wskaźników nie jest równa “k” to wtedy musimy podzielić surowe wskaźniki sezonowości przez współczynnik korygujący (suma wskaźników surowych / k). Otrzymany w ten sposób czyste wskaźniki sezonowości.
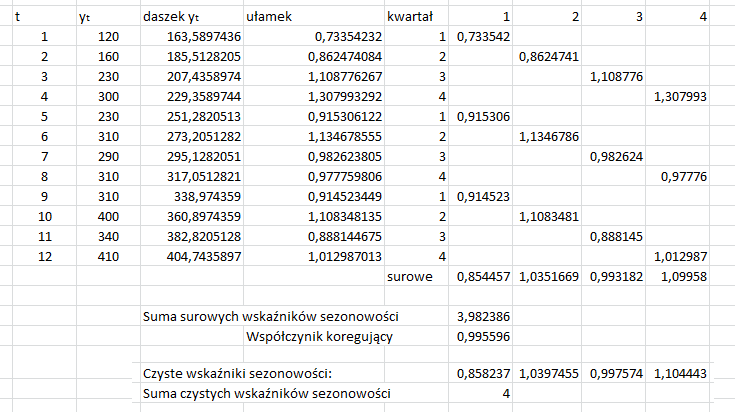
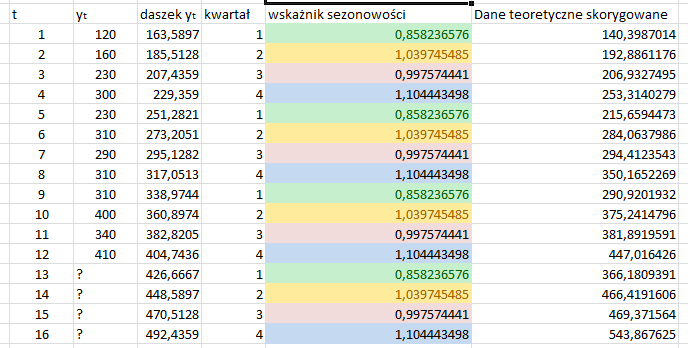
Oto cała tabelka przedstawiające te zagadnienie.
Dane są identyczne z poprzedniego wpisu dlatego wartości teoretyczne zostały już policzone wcześniej. Nie trafnie nazwałem “wielkość wahań okresowych” w tej tabelce ,ale jest jak już pisałem wcześnie jest to ułamek “wartości z szeregu” z wartościami teoretycznymi.
Wzór na surowy wskaźnik sezonowości jest następujący gdzie “i” jest numerem okresu należącej do tej samej fazy. Mówiąc prościej surowy wskaźnik sezonowości dla danego kwartału gdzie “i” jest numerem kwartału.
Wielkość wahań okresowych dopisujemy do odpowiednich kwartałów.
Później te kwartały sumujemy w następujący sposób otrzymując 4 wskaźniki surowych sezonowości.
Sumujemy surowe wskaźniki sezonowości.
Jak widać suma nie równa 4. Czyli przechodzą do następnego kroku. Wyliczam współczynnik korygujący.
Jak widać na obrazku poniżej umiem pisać poprawnie po polsku słowo “korygujący”. ![]()
Dzielący każdy wskaźnik surowej sezonowości przez współczynnik korygujący otrzymuje teraz “czyste wskaźniki sezonowości”.
Teraz zadajemy sobie pytanie po co nam te “czyste wskaźniki sezonowości”.

Jeżeli pomnożymy w każdym okresie teoretyczny poziom zjawiska “yˆt” przez odpowiedni dla danego okresu wskaźnik sezonowości, to otrzymamy teoretyczny poziom zjawiska uwzględniający wahania sezonowe.
Mówiąc prościej mając wskaźnik sezonowości jesteśmy wstanie bardziej dokładnie przewidzieć przyszłość używając funkcji liniowej trendu.
Jak widać wskaźniki sezonowości się powtarzają ponieważ są symbolizują one dany kwartał.
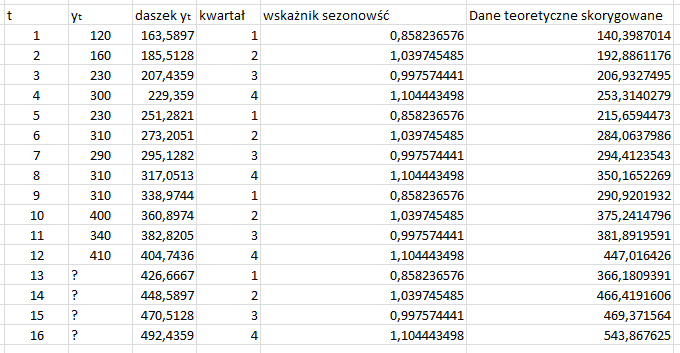
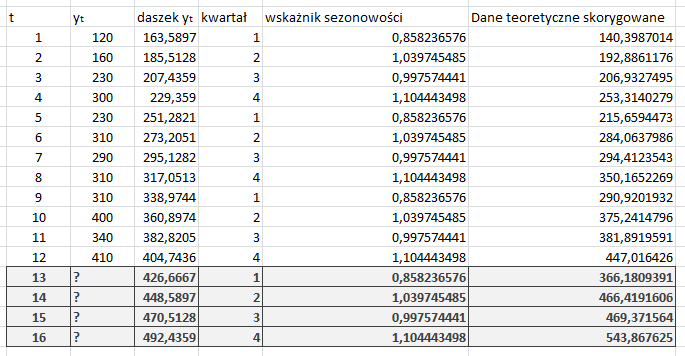
Mając “wskaźniki sezonowości” jesteśmy wstanie policzyć dane teoretyczne skorygowane.
W teorii dzięki temu lepiej możemy przewidzieć przyszłość dla “13,14,15,16” miesiąca lub jak kto woli dla następnego kwartału.
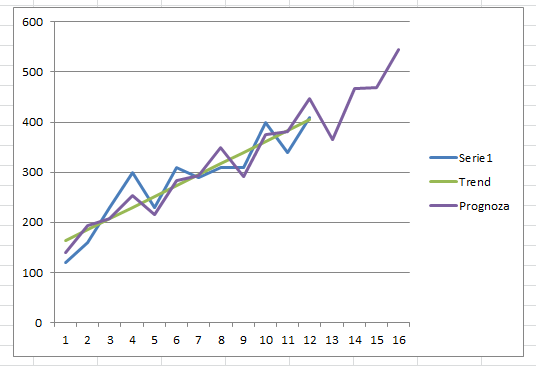
Oto wynik graficzny funkcji trendu oraz prognozy na podstawie danych teoretycznie skorygowanych.
Jeśli czytałeś wpis początkowy to wiesz ,że ten wpis powstał tylko dla tego ,że próbuje odszyfrować prezentacje z szeregów czasów na podstawie innej prezentacji która jest dla mnie bardzie czytelna.
Niestety oryginalna prezentacja mówi także o wahaniach okresowych gdy nie mamy trendu. Gdzie “i” zapewne jest numerem okresu należącej do tej samej fazy.
W prezentacji występuje podział na szereg addytywny i multiplikatywny i zależność od tego podziału są inne wzory. Wszystko to co zostało policzone wcześniej jest dla szeregu multiplikatywnego zapewne. Wzory z dwóch prezentacji nie nakładają się na siebie mimo iż w teorii opisują to samo zagadnienie. Jak tutaj nie być zakłopotany. Z drugiej strony jest to przedmiot który zakłada ,że 2 godzinny może się nauczyć algorytmów genetycznych więc mnie to nie dziwi.