Dimension-X Algorytmy centroidów. K-Średnie.
Postanowiłem poświęcić im kolejny wpis na blogu. W poprzednim wpisie napisałem kod dla przestrzeni 2 wymiarowej XY. Jednak ten algorytm staje się dopiero użyteczny, gdy zwiększymy liczbę wymiarów.
Przerobienie swojego kodu z poprzedniego wpisu odbyło dosyć szybko. Napisanie tego wpisu zajmie mi zapewne więcej czasu.
O co chodzi z wymiarami i algorytmem K-Średnich? Po co na tyle wymiarów?
Kiedyś oglądałem Transformersów w jednym wymiarze 1-D. Było super.
Do czego ten algorytm może się przydać? Jak on działa?
Na te pytania odpowiedziałem już w poprzednim wpisie. Ba nawet narysowałem parę ilustracji objaśniający problem.
Co więc trzeba było przerobić ,aby ten algorytm działał dla nieokreślonej liczby wymiarów niż tylko dwóch.
Zacznijmy od definicji punktu. Skoro możemy mieć nieokreśloną liczbę parametrów X logicznie jest potraktowanie ich jako listy. Dla 5 wymiarów byśmy mieli parametry X1,X2,X3,X4,X5. Kluczem do tego rozwiązania jest jego elastyczność. Poza tym dynamiczne właściwości wymagają niezłej refleksji dlatego lista jest dobrym i prostym rozwiązaniem.
[Serializable]
public class Punkt
{
public Punkt(int wymiary)
{
X = new List<double>(wymiary);
}
public Punkt()
{
X = new List<double>(Wymiary);
}
public static int Wymiary = 10;
public List<double> X { get; set; }
public int Grupa { get; set; }
public double this[int i]
{
get
{
if ((X.Count > i) && (i >= 0))
return X[i];
throw new ArgumentException();
}
set
{
if ((X.Count > i) && (i >= 0))
X[i] = value;
else
throw new ArgumentException();
}
}
}Dla ułatwienia sobie życia klasa Punkt zawiera w sobie indekser. Indekser wskazuje na element na liście “X-ów”.
Czyli pisząc przykładowo “punkt[3]” będę się dowoływał do czwartego punktu na liście X. Dlaczego czwartego, ponieważ lista zaczyna swoją numeracje od zera.
Dodałem też pole statyczne określające ile z góry elementów ma być zadeklarowanych na liście. Domyślnie lista deklaruje miejsce na 10 elementów.
Klasa punkt musi mieć atrybut “Serializable”, gdyż później będę klonowana.
W pierwszym kroku algorytmu zapamiętujemy listę “k” punktów. W składni tego kodu nic się nie zmieniło poza tym ,że postanowiłem nie dzielić klasy “punkt”. Klas punkt teraz reprezentuje i “k” punkt, jak i punkt wynikające z danego zbioru danych.
public static object DeepClone(object obj)
{
object objResult = null;
using (MemoryStream ms = new MemoryStream())
{
BinaryFormatter bf = new BinaryFormatter();
bf.Serialize(ms, obj);
ms.Position = 0;
objResult = bf.Deserialize(ms);
}
return objResult;
}
private static List<Punkt> memeory = new List<Punkt>();
public static void ZapamietajOstatniePolozenieKPunkt(List<Punkt> kpunkty)
{
memeory = new List<Punkt>();
memeory = (List<Punkt>)DeepClone(kpunkty);
}Zerowanie grup też nie uległo zmianie.
public static void ZerowanieGrup(ref List<Punkt> zbior)
{
foreach (var punkt2 in zbior)
{
punkt2.Grupa = -1;
}
}Nadanie grupy też nie uległo zmianie, ponieważ ta metoda operuje na liście punktów ,a nie na samym punkcie.
public static void NadanieGrupZbiorowi(ref List<Punkt> zbior, List<Punkt> kpunkty)
{
for (int i = 0; i < zbior.Count; i++)
{
Punkt punkt2 = zbior[i];
NadanieGrupy(ref punkt2, kpunkty);
}
}Teraz gdy operujemy na klasie punkt musimy dokonać pewnych drobnych zmian. Filozofia liczenia odległości nie uległa zmianie. Skoro operujemy na liście X naturalnie powinniśmy otrzymać listę różnić współrzędnych punktów X.
Ostatecznie odległość pomiędzy punktami mającymi X współrzędnych wynika z ich sumy różnic podniesionych do kwadratu. Później ta suma musi być spierwiastkowana. Dla przypomnienia wzór.
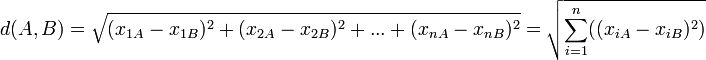
Metoda nadająca grup nie uległa zmianie.
public static double LiczenieOdleglosc(Punkt p1, Punkt p2)
{
List<double> wyniki = new List<double>();
for (int i = 0; i < p1.X.Count; i++)
{
wyniki.Add(Math.Pow(p1[i] - p2[i], 2));
}
double a = Math.Sqrt(wyniki.Sum());
return a;
}
public static void NadanieGrupy(ref Punkt punkt, List<Punkt> kpunkty)
{
Dictionary<double, Punkt> d = new Dictionary<double, Punkt>();
foreach (var kpunkt in kpunkty)
{
double od = LiczenieOdleglosc(kpunkt, punkt);
while (d.ContainsKey(od))
{
od = od + 0.000001;
}
d.Add(od, kpunkt);
}
var g = d.First(k => k.Key == d.Keys.Min()).Value.Grupa;
punkt.Grupa = g;
}Przesuniecie punktu uległo małej poprawce. Indekser, który napisałem wcześniej teraz pokazuje swoją prawdziwą użyteczność. W połączeniu z wyrażeniem LINQ “Average” średnia nieokreślonej liczby współrzędnych “X” wykonuje się gładko.
public static void PrzesunieciePunkuK(List<Punkt> zbior, ref List<Punkt> kpunkty)
{
foreach (var kpunkt in kpunkty)
{
List<Punkt> punkty = new List<Punkt>();
foreach (var punkt in zbior)
{
if (punkt.Grupa == kpunkt.Grupa)
{
punkty.Add(punkt);
}
}
double x1 = 0;
double x2 = 0;
if (punkty.Count > 0)
{
List<double> srednia = new List<double>();
for (int i = 0; i < punkty[0].X.Count; i++)
{
srednia.Add(punkty.Average(k => k[i]));
}
kpunkt.X = srednia;
}
}
}Metoda czy punkt się zmieniły musiała ulec zmienić gdyż operujemy na liście współrzędnych. Kod o dziwo jest teraz bardziej czytelny.
public static bool CzyPunktySieZmienily(List<Punkt> kpunkty)
{
bool yes = true;
for (int i = 0; i < kpunkty.Count; i++)
{
for (int j = 0; j < kpunkty[i].X.Count; j++)
{
if (Math.Abs(kpunkty[i].X[j] - memeory[i].X[j]) > double.Epsilon)
{
yes = false;
}
}
}
return yes;
}Sam algorytm oczywiście nie uległ zmianie.
public static int AlgoStart(ref List<Punkt> punkty, ref List<Punkt> kpunkty, int counterStop)
{
int counter = 0;
while (counter < counterStop)
{
KSrednieMetody.ZapamietajOstatniePolozenieKPunkt(kpunkty);
KSrednieMetody.ZerowanieGrup(ref punkty);
KSrednieMetody.NadanieGrupZbiorowi(ref punkty, kpunkty);
KSrednieMetody.PrzesunieciePunkuK(punkty, ref kpunkty);
if ((KSrednieMetody.CzyPunktySieZmienily(kpunkty)))
{
break;
}
counter++;
}
return counter;
}Teraz sprawdźmy czy otrzymam takie same wyniki jak w moim programie dla K-Średnich na przestrzeni dwumiarowej.
using System;
using System.Collections.Generic;
namespace KSrednieNWymiarowe
{
class Program
{
static void Main(string[] args)
{
Punkt.Wymiary = 2;
List<Punkt> kpunkty = new List<Punkt>();
kpunkty.Add(new Punkt() { X = new List<double>() { 0, 1}, Grupa = 1}) ;
kpunkty.Add(new Punkt() { X = new List<double>() { 2, -1 }, Grupa = 2 });
kpunkty.Add(new Punkt() { X = new List<double>() { 6, -2 }, Grupa = 3 });
List<Punkt> punkty = new List<Punkt>();
punkty.Add(new Punkt() { X = new List<double>() { -7, 5 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { -5, 3 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { -6, 1 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { -3, -1 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { -5, -3 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { 3, 7 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { 2, 2 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { 8, 5 }, Grupa = -1 });
punkty.Add(new Punkt() { X = new List<double>() { 10, 4 }, Grupa = -1 });
int amount = KSrednieMetody.AlgoStart(ref punkty, ref kpunkty, 100);
Console.WriteLine("\nPunkty: \n");
foreach (var punkt in punkty)
{
Console.WriteLine("\t ");
int c = 1;
foreach (var x in punkt.X)
{
Console.Write(" X{0}: {1}", c, x);
c++;
}
Console.Write(" Grupa: " + punkt.Grupa);
}
Console.WriteLine("\n\nK punkty: \n");
foreach (var punktK in kpunkty)
{
Console.WriteLine("\t ");
int c = 1;
foreach (var x in punktK.X)
{
Console.Write(" X{0}: {1}", c, x);
c++;
}
Console.WriteLine(" Grupa: " + punktK.Grupa);
}
Console.WriteLine("\nLiczba pętli: " + amount);
Console.ReadKey();
}
}
}Wyniki są identycznie więc algorytm po przeróbce działa tak samo. ![]()



