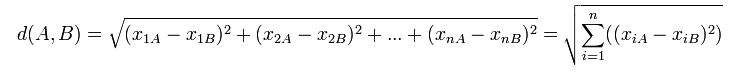K-meansAlgorytm centroidów służy do analizy skupień. Przykładowo na osi XY mamy zbiór punktów i chcemy określić czy pewne punkty są odpowiednio skupione do siebie.
Jeżeli punkty są skupione uznajemy ,że reprezentują one pewną grupę.
Oczywiście możesz zadać pytanie do czego może się to przydać. Algorytm ten jest prosty ,a jego moc polega na tym ,że potrafi on łatwo zlokalizować grupy na osi X-wymiarowej.
Na osi XY gołym okiem jesteśmy zaobserwować skupiska punktów. Niestety, ponieważ nasza rzeczywistość nie jest hipersześcianowa nie jesteśmy wstanie zlokalizować skupisk punktów dla przestrzeni 9000 wymiarowej. Po co nam ,aż 9000 wymiarów?
Kiedyś oglądałem Epokę Lodowcową w 6 wymiarze i było fajnie.
 Punkty a osi X-wymiarowej określają na zbiory cech. Mając ich odpowiednio dużo możemy otrzymać odpowiednio dobre wyniki. Możemy określić ,że przedmioty zawierające właśnie te cechy są zbliżone do siebie i mogą być pogrupowane.
Punkty a osi X-wymiarowej określają na zbiory cech. Mając ich odpowiednio dużo możemy otrzymać odpowiednio dobre wyniki. Możemy określić ,że przedmioty zawierające właśnie te cechy są zbliżone do siebie i mogą być pogrupowane.
Jako webdeveloper nie powinien interesować się takimi rzeczami. Wiecie moja uwaga powinna koncentrować się Jquer-ach, CSS-ach ,ASP.NET-ach ,ale od czego są studia.
Dla wszystkich, którzy mają problem ze zrozumienie algorytmy centroidów postanowiłem napisać prosty kod, który wykonuje ten algorytm na przestrzenie dwuwymiarowej. Kto wiem może kiedyś mi się to też przyda. Chętnie bym poczytał swoje notatki na temat algorytmów genetycznych ze studiów inżynierskich, gdyby je miał.
K Średnie Na czym polega algorytm
Algorytm składa się on z następujący kroków.
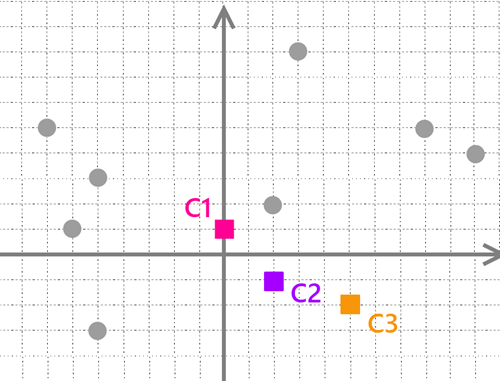
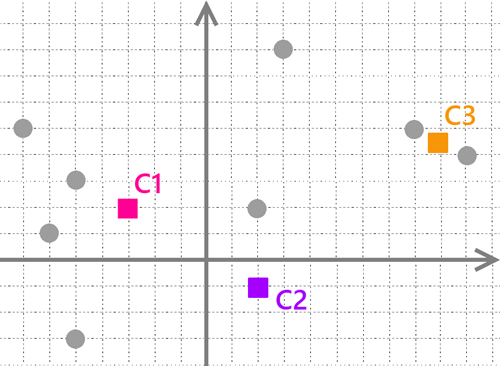
Mamy zbiór szarych punktów rozmieszczonych po osi dwu wymiarowej. Naszym zadaniem jest ustalenie dla nich 3 grup.
Pierwszym krok algorytmu polega na wyborze punktów “K” (kwadraty). Te punkty będą określać grupy dla pozostałych punktów. Współrzędne startowe punktów mogą wpływać na wyniki końcowy. W tym wypadku zostały one wybrane losowo.
W drugi kroku ustalamy grupy szarych punktów względem punktów “K”.
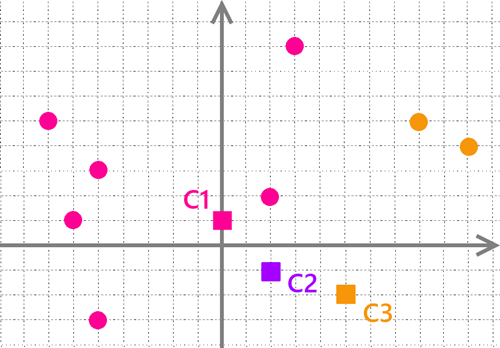
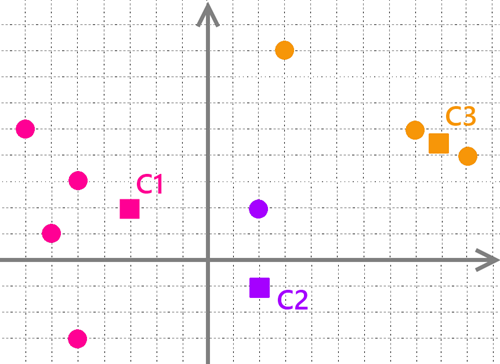
Jak ustalamy grupy? Sprawdzamy odległość szarego punkta od punktów “K”. Najbliższy punkt “K” ustala grupę. Analogicznie postępujemy dla pozostałych szarych punktów. Jak widzisz na poniższym obrazku grupy zostały określone jako kolory. Wynik tego kroku wygląda tak.
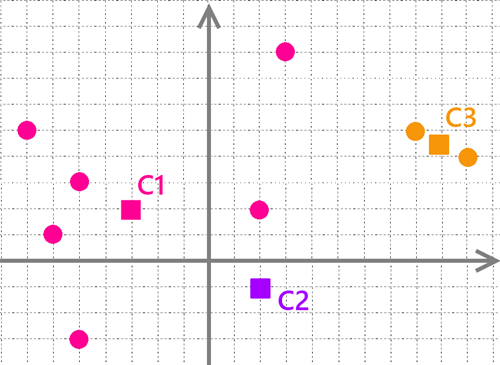
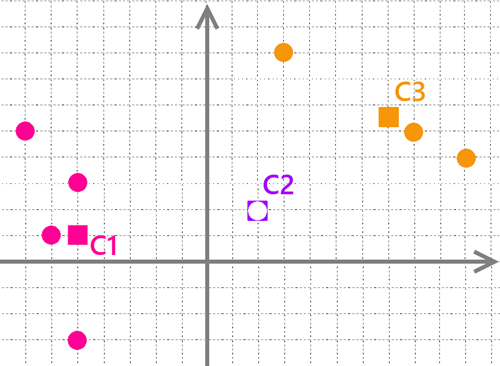
Trzeci krok polega na przesunięciu punktów “K”.
Nowe współrzędne punktu “K” to średnia arytmetyczna współrzędnych wszystkich punktów mając jego grupę. Jak widać w wyniku tego kroku punkt “K C3” znajduje się pomiędzy punktami należącymi do jego grupy. Natomiast punkt “K C2” nie został przesunięty, ponieważ nie ma on żadnych przypisanych punktów.
W czwartym kroku sprawdzamy czy punkty “K” zmieniły swoje położenie wyniku poprzedniego kroku. Jeśli tak to algorytmy trwa. Zerujemy grupy punktów i powtarzamy proces.
Znowu wybieramy grupy względem najbliższego punktu “K”.
Potem przesuwanym punkty “K” względem średniej arytmetycznej wszystkich współrzędnych.Punkt “K C2” ma tylko jeden punkt z grupy więc ten punkt “K” ma takie same współrzędne jak ten punkt.
Punkty “K” znowu zmieniły swoje położenie więc algorytm trwa nadal. Dalsze etapy powielają poprzedni wynik i punkty “K” nie ulegają zmianie. Algorytm się kończy.
Kod C#
Na potrzeby tego wpisu napisałem prostą aplikację konsolową oraz zestaw metod liczących ten algorytm dla przestrzeni dwuwymiarowej. Jeśli chcesz uzyskać kod dla większej ilości wymiarów wystarczy tylko zwiększyć liczbę punktów “X” gdyż filozofia kodu się nie zmienia.
Postanowiłem też w kodzie użyć polskich nazw. W programowaniu jest bardzo kiepski pomysł ,ale dla nowicjusza przynajmniej kod stanie trochę czytelniejszy. ![]()
Klasy reprezentujące punkty są następujące. Obie klasy muszą mieć atrybut “Serializable”, ponieważ później ułatwia mi to klonowanie kolekcji punktów. Różnica pomiędzy klasą “punkt” ,a “punktK” polega tylko na tym ,że współrzędne zwykłego punktu są liczbami całkowitymi. Naturalnie możesz śmiało odrzuć ten pomysł i mieć jedna klasę “Punkt”.
using System;
namespace KSrednieDwaWymiary
{
[Serializable]
public class Punkt {
public int X1 { get; set; }
public int X2 { get; set; }
public int Grupa { get; set; }
}
[Serializable]
public class PunktK {
public double X1 { get; set; }
public double X2 { get; set; }
public int Grupa { get; set; }
}
}Pisanie algorytmu zaczynamy od zapamiętywania współrzędnych punktów K z ostatniej iteracji. Jak widać mamy prywatną listę punktów “K,”, która dzięki metodzie “ZapamietajOstatniePolozenieKpunkt” stanie się idealną kopią obecnych punktów “K” .
Dla przypomnienia operacja przyrównania obiektów czy kolekcji kończy się tylko na kopiowaniu jej referencji. Obie zmienne referowałyby się do tego samej kolekcji obiektów. Dlatego muszę klonować listę punktów.
Robi ten algorytm trochę od końca ,ale lista sklonowanych punktów K będzie potrzebna później do sprawdzenia czy punkt “K” uległy przesunięciu w wyniku operacji algorytmu K-Średnich.
public static object DeepClone(object obj)
{
object objResult = null;
using (MemoryStream ms = new MemoryStream())
{
BinaryFormatter bf = new BinaryFormatter();
bf.Serialize(ms, obj);
ms.Position = 0;
objResult = bf.Deserialize(ms);
}
return objResult;
}
private static List<PunktK> memeory = new List<PunktK>();
public static void ZapamietajOstatniePolozenieKPunkt(List<PunktK> kpunkty)
{
memeory = new List<PunktK>();
memeory = (List<PunktK>)DeepClone(kpunkty);
}Zgodnie z algorytmem po każdej iteracji zerujemy grupy. W kodzie grupy są reprezentowane poprzez liczby. Zakładamy ,że grupa –1 nie reprezentuje żadnego istniejącego punktu “K”.
W metodzie użyłem słowa kluczowego “ref”. Oznacza to ,że do metody jest wysłana oryginalna referencja kolekcji i wyniku działania metody ulegnie ona zmianie. Bez użycia słowa “ref” metoda by operowałaby na tymczasowej kopi kolekcji nie zmieniając zawartości jej oryginału.
public static void ZerowanieGrup(ref List<Punkt> zbior)
{
foreach (var punkt2 in zbior)
{
punkt2.Grupa = -1;
}
}Gdy już wyzerowaliśmy grupy przechodzimy do głównych dwóch kroków algorytmu centroidów czyli do “nadawania grup” oraz przesuwania punktów K.
Nadanie grupy zmieni nam kolekcje zwykłych punktów więc są one przekazywane do metody jako referencja. Dla każdego punktu wywołuje metodę “NadanieGrupy” w której pojedynczy punkt też jest wysłany jako referencja.
public static void NadanieGrupZbiorowi(ref List<Punkt> zbior, List<PunktK> kpunkty)
{
for (int i = 0; i < zbior.Count; i++)
{
Punkt punkt2 = zbior[i];
NadanieGrupy(ref punkt2, kpunkty);
}
}W metodzie “NadanieGrupy” tworze słownik, w którym kluczami będą odległości.
Dlaczego to robię?
Z algorytmem K-Średnich jest jeden problem. Jeśli uzyskamy podobne odległości dla kilku punktów “K” jak mamy wtedy określić grupę dla punktu?
Ja postanowiłem każdą następną podobną odległość zwiększać o niewielki ułamek. Robię to w pętli while, ponieważ powtórzenie może wystąpić więcej niż raz. Trzeba także pamiętać o tym ,że liczby double,float i tak dalej są porównywane poprzez zaokrąglenie. Dlatego n.p nie zwiększam odległość o epsilon czy inną naprawdę małą wartość, ponieważ wtedy nasz algorytm utkwi w pętli “while”.
Liczba 0.000001 nie jest za duża aby wpłynęła negatywnie na wyniki algorytmu ,a zarazem nie jest za mała aby algorytm się nie zawiesił przy pętli while.
public static double LiczenieOdleglosc(PunktK p1, Punkt p2)
{
var x = Math.Pow(p1.X1 - p2.X1, 2);
var x2 = Math.Pow(p1.X2 - p2.X2, 2);
double a = Math.Sqrt(x + x2);
return a;
}
public static void NadanieGrupy(ref Punkt punkt, List<PunktK> kpunkty)
{
Dictionary<double, PunktK> d = new Dictionary<double, PunktK>();
foreach (var kpunkt in kpunkty)
{
double od = LiczenieOdleglosc(kpunkt, punkt);
while (d.ContainsKey(od))
{
od = od + 0.000001;
}
d.Add(od, kpunkt);
}
var g = d.First(k => k.Key == d.Keys.Min()).Value.Grupa;
punkt.Grupa = g;
}Używając LINQ ze słownika wybieram najmniejszy klucz. Na podstawie tego klucza wybieram punkt “K” ,a z punkt “K” przypisuje jego grupę do danego punktu.
A co z liczeniem odległości. Jak widać studia każdego odmóżdżyły od podstawowej matematyki. ![]()
Wzór jest następujący. Odległość punktu to różnica jego współrzędnych podniesiona do kwadratu po czym dodana i z pierwiastkowana. Dla większej ilości współrzędnych wzór nie bardzo się zmienia i jest zdecydowana zaleta tego algorytmy.
Punkty mają już swoje grupy. Teraz musimy przesuwać punkty K względem nich.
Tworzę kolekcję punktów należący tylko do odpowiedniej grupy punktu K. Jeśli kolekcja ta nie jest pusta to przy pomocy metody “Avarage” wyciągam z niej średnią arytmetyczną współrzędnych X1 i X2.
Punkt “K” ma teraz punkty wynikającej ze średniej.
public static void PrzesunieciePunkuK(List<Punkt> zbior, ref List<PunktK> kpunkty)
{
foreach (var kpunkt in kpunkty)
{
List<Punkt> punkty = new List<Punkt>();
foreach (var punkt in zbior)
{
if (punkt.Grupa == kpunkt.Grupa)
{
punkty.Add(punkt);
}
}
double x1 = 0;
double x2 = 0;
if (punkty.Count > 0)
{
x1 = punkty.Average(i => i.X1);
x2 = punkty.Average(i => i.X2);
kpunkt.X1 = x1;
kpunkt.X2 = x2;
}
}
}Na koniec algorytmu sprawdzamy czy chociaż jeden z punktów K zmieniły swoje położenie od ostatniej iteracji. Tutaj właśnie pojawia się kolekcja punktów “K” “memory”, która została sklonowana na bazie punktów sprzed zmiany.
public static void PrzesunieciePunkuK(List<Punkt> zbior, ref List<PunktK> kpunkty)
{
foreach (var kpunkt in kpunkty)
{
List<Punkt> punkty = new List<Punkt>();
foreach (var punkt in zbior)
{
if (punkt.Grupa == kpunkt.Grupa)
{
punkty.Add(punkt);
}
}
double x1 = 0;
double x2 = 0;
if (punkty.Count > 0)
{
x1 = punkty.Average(i => i.X1);
x2 = punkty.Average(i => i.X2);
kpunkt.X1 = x1;
kpunkt.X2 = x2;
}
}
}Warto tutaj zwróci uwagę ,że nie porównuje liczby double bezpośrednio tylko sprawdzam czy różnica tych liczb jest większa niż epsilon (najmniejsza liczba double dostępna dla środowiska .NET). Tak jak mówiłem wcześniej normalne porównywanie zaokrągla na liczby do pewnego stopnia co oznacza ,że możemy mieć zafałszowany wyniki.
Mamy już metody. Teraz musimy połączy je w jakąś sekwencję. Metoda całego algorytmu wygląda tak. Jak widać wszystkie metody są statyczne i zawierają się w klasie “KSrednieMetody”.
Jeśli metoda “CzyPunktySieZmienily” zwróci prawdę wtedy pętla zostanie przerwana wyniku słowa kluczowego “break”. Do głównej pętli while dodałem możliwość zatrzymania całego algorytmu, jeśli zostanie przekroczona odpowiednia ilość iteracji.
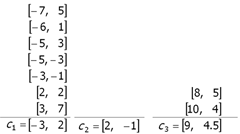
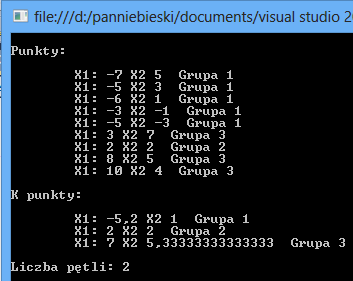
Mamy już kod liczący algorytm centroidów. Sprawdźmy czy jeśli umieścimy w nim takie same dane jak w przykładzie graficznym to otrzymamy podobne wyniki.
Kod aplikacji konsolowej używającej metody klasy “KSrednieMetody” jest taki.
using System;
using System.Collections.Generic;
namespace KSrednieDwaWymiary
{
class Program
{
static void Main(string[] args)
{
List<PunktK> kpunkty = new List<PunktK>();
kpunkty.Add(new PunktK() { X1 = 0, X2 = 1, Grupa = 1 });
kpunkty.Add(new PunktK() { X1 = 2, X2 = -1, Grupa = 2 });
kpunkty.Add(new PunktK() { X1 = 6, X2 = -2, Grupa = 3 });
List<Punkt> punkty = new List<Punkt>();
punkty.Add(new Punkt() { X1 = -7, X2 = 5 });
punkty.Add(new Punkt() { X1 = -5, X2 = 3 });
punkty.Add(new Punkt() { X1 = -6, X2 = 1 });
punkty.Add(new Punkt() { X1 = -3, X2 = -1 });
punkty.Add(new Punkt() { X1 = -5, X2 = -3 });
punkty.Add(new Punkt() { X1 = 3, X2 = 7 });
punkty.Add(new Punkt() { X1 = 2, X2 = 2 });
punkty.Add(new Punkt() { X1 = 8, X2 = 5 });
punkty.Add(new Punkt() { X1 = 10, X2 = 4 });
int counter = 0;
int amount = KSrednieMetody.AlgoStart(ref punkty,ref kpunkty, 100);
Console.WriteLine("\nPunkty: \n");
foreach (var punkt in punkty)
{
Console.WriteLine("\tX1: " + punkt.X1 + " X2 " + punkt.X2 + " Grupa " + punkt.Grupa);
}
Console.WriteLine("\nK punkty: \n");
foreach (var punktK in kpunkty)
{
Console.WriteLine("\tX1: " + punktK.X1 + " X2 " + punktK.X2 + " Grupa " + punktK.Grupa);
}
Console.WriteLine("\nLiczba pętli: " + amount);
Console.ReadKey();
}
}
}Wyniki są identyczne.
Być może w przyszłości poprawie ten kod ,aby można było liczyć “K-Średnie” dla nieokreślonej liczby wymiarów. Można teraz co prawda dodawać do kodu parametry X12-X13-X(N) ,ale nie dodaje to żadnej elastyczności do kodu.